Retranscrire le ladder en littéral: les équations logiques.
Alors comment ça se passe avec l’anglais? Pas trop mal j’espère car on en aura de besoin (je vous rassure ça restera light). Le littéral est plus condensé que le ladder et réclame un peu plus d’imagination. Allons y par étape, rappelez vous notre premier programme:
1 contact NO en série avec 1 sortie
En littéral, on écrit:
DO := DI1;
Traduction, lorsque j’ai DI1 à 1, j’ai DO à 1: donc DO := DI1; . Jusque la, c’est plutôt simple. On peut clairement voir que DO aura toujours le même état que DI1, cela dit n’oubliez pas les : avant le égal, et le point virgule.
1 contact NC au repos en série avec une sortie
En littéral, on écrit:
DO:= NOT DI2:
Passons à nos deux contacts en série.
Dans cette ligne, DO est activée lorsque DI1 sera au travail et qu’aucune action n’est exercée sur DI2, d’où le NOT pour indiquer que le résultat de DO sera l’inverse de DI2.
1 contact normalement ouvert en série avec 1 contact normalement fermé en série avec 1 sortie
En littéral, on écrit:
DO := DI1 AND NOT DI2;
Table de vérité
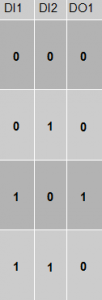
On complique légèrement les choses. Lorsqu’il commence à y avoir trop d’éléments, il peut être utile de ressort la table de vérité.
On y lit que la sortie n’est activée que lorsque j’ai une action sur DI1 ET PAS DI2.
(voir la 3e ligne)
soit: DO := DI1 AND NOT DI2;
Bon, on va aller sur codesys pour faire un petit break.
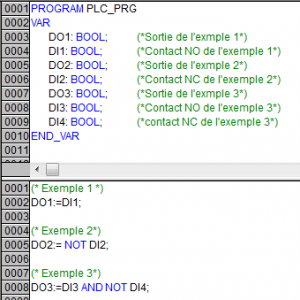
Créez un nouveau programme, mais cette fois au lieu de choisir LD dans le langage de l’unité, vous sélectionnerez ST (pour Strutured Literall). Nous allons réaliser les 3 exemples avec des variables différentes. Utilisez donc DI1 et DO1 pour l’exemple 1, DI2 et DO2 pour le suivant et enfin DI3, DI4 et DO3 pour le dernier exemple, et faites vos essais.
Sachez qu’en littéral vous pouvez mettre des commentaires dans le programme. Abusez en !
Exemples en littéral
Vous allez commencer à apprécier réellement les commentaire 🙂
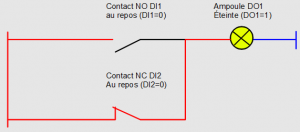
On continu avec nos contacts en parallèle, avez vous une idée de comment retranscrire cela en littéral?
1 contact NO au repos en parallèle avec 1 contact NC au repos
En littéral, on écrit:
DO1 := DI1 OR NOT DI2;
Continuons de « lire » le schéma. Pour que DO1 s’active, il faut soit passer DI1 au travail OU laisser DI2 au repos (les deux situations alimentent DO1), d’où:
DO1 := DI1 OU PAS DI2, soit DO1 := DI1 OR NOT DI2;
Table de vérité
Bonus: le paragraphe qui suit est un petit plus, passez directement au suivant si vous vous sentez dépassé.
(Cette explication sera « ultra-simplifiée ». Le but étant de vous montrer outil du Tableau de Karnaugh. Si cela vous intéresse, faites le savoir sur le forum et je ferai peut être un mini-tuto là dessus).
Il est un peu plus compliqué d’utiliser la table de vérité ici. En effet, il faudrait écrire chaque situation où DO1 est à 1 séparée d’un OR, ce qui ressemblerai à:
DO1:= (NOT DI1 AND NOT DI2) OR (DI1 AND NOT DI2) OR (DI1 AND DI2);
(croyez moi, cette équation est égale à DO1 := DI1 OR NOT DI2 😉 )
Pour simplifier cette équation complexe, il existe plusieurs métodes, mais ma favorite étant celle du tableau de Karnaugh.
Tableau de karnaugh
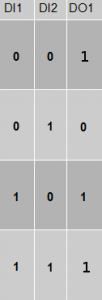
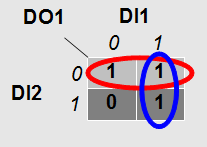
Le but consiste à mettre les différents états possibles associés au lignes et colonnes d’un tableau. Dans notre exemple l’horizontal représente les états possibles de DI1, et la vertical représente DI2.
A l’intérieur de celui ci, il faut noter l’état de la sortie dans chacune des situations. Dans notre cas, le seule situation pour que la sortie soit éteinte est que DI1 soit au repos et que DI2 soit au travail, donc aux coordonnées DI1 à 0 et DI2 à 1 nous inscrivons 0. Ce qui nous donne un tableau, remplit de trois 1 et d’un 0 pour DI1=0 et DI2=1.
Ensuite, il faut encercler tous les 1 se trouvant à la vertical et à l’horizontal. Ici nous avons deux possibilités, entourées en rouge et en bleu. Puis pour chacun de ses cercles, il faut repérer la variable qui ne change pas d’état.
Pour le cercle rouge, on voit que pour les deux situations, DI2 reste à zéro, et pour le cercle bleu, c’est DI1 qui reste à 1.
Et bien avec ce que l’on vient de relever, il suffit de les séparer d’un « OU » les 2 variables et de mettre un « NOT » devant celle restant à 0 pour avoir notre solution:
DO1 := DI1 OR NOT DI2;
Qui reste plus simple que: DO1:= (NOT DI1 AND NOT DI2) OR (DI1 AND NOT DI2) OR (DI1 AND DI2);
qui est pourtant rigoureusement la même chose.
Bon ce fût peut être un peu brouillon, mais n’étant pas l’objet du chapitre je ne veux pas perdre trop de temps la dessus. Maintenant si c’est un sujet qui vous intéresse, faite le moi savoir via le forum et j’essaierai d’en faire un tuto à part entière.
Voila si vous aviez sauter le paragraphe sur le tableau de Karnaugh, vous pouvez revenir.
Nous venons de voir ce qu’étaient les variables et les équations logiques en littéral. Sans parler du tableau de Karnaugh, cette partie n’a pas du être trop éprouvante pour vous, voici les choses à retenir:
-
Le mot clé pour mettre deux contacts en série est AND.
-
Le mot clé pour mettre deux contacts en parallèle est OR.
-
Le mot clé pour « normalement fermé » est NOT.
Maintenant que vous avez ces bases, passons à quelque chose de plus intéressant dans ce tutoriel programmation littéral: les structures conditionnelles.