Tutoriel programmation: du ladder au littéral
Une page se tourne. L’initiation à la programmation est terminée, maintenant vous allez réellement programmer. Dans un premier temps, je vous présenterai les variables analogiques, qui contrairement aux variables Tout Ou Rien, peuvent contenir de (très) grand nombres. Ensuite, avec les notions de logique combinatoire que vous aurez acquis, nous pourrons passer aux choses sérieuses, la programmation en littéral. Dans ce chapitre, vous apprendrez vos premiers mot-clés, que nous substituerons à nos programmes fait en ladder. Cette partie sera plus légère que la précédente afin de vous éviter un claquage cérébrale 🙂 . Allez c’est parti.
Note: si vous n’avez pas installé Codesys, le logiciel que nous utilisons pour nous exemple, voici le lien expliquant la procédure à faire: Lien pour télécharger et installer codesys.
Voici un lien vers le chapitre précédent, « la mémoire des ampoules » cliquez ici.
Vidéo, partie 1: Les variables analogiques:
Vidéo, partie 2: Le littéral structuré et les IF / ELSIF / ELSE:
Les variables analogiques.
Vous connaissez les variables Booléennes, qui se limites aux valeurs 0 et 1, maintenant vous allez découvrir quelques uns des différents type de variables analogiques.

Signal analogique: source Wikipédia
Compter en binaire.
Petite précision de vocabulaire: binaire = booléen = Tout Ou Rien = bit.
De la même façon que l’on compte avec nos nombres décimaux(0,1,2,3,4,5,6,7,8,9,10,11,12…), on compte aussi en binaire.
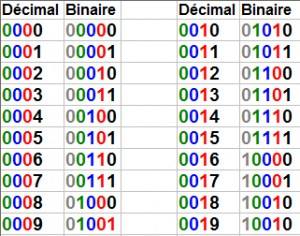
Avec le système décimal, vous commencez à compter de 0 jusque 9, puis vous ajouter le 1 des dizaines pour compter de 10 jusque 19, puis vous ajouter le 2 des dizaines pour aller de 20 a 29 . . . . puis les centaines en remettant les dizaines à 0 pour compter de 100 à 109 . . . etc. Et bien en binaire c’est pareil, mais avec 2 chiffres, le 0 et le 1. Les premiers nombre sont donc 0, 1 puis ayant fait le tour de nos possibilités, on incrémente le champs de gauche, ce qui fait 10, 11. La encore, toutes les combinaisons ayant été exécutée, on incremente le champs de gauche suivant avec 100, 101, 110, 111, puis en continue ainsi de suite avec 1000, 1001… Voici l’évolution du système de comptage binaire.
Astuce: La calculatrice Windows fait la conversion de binaire en décimal, pour ceci démarrez la et dans affichage choisissez "Programmeur". Dans l'un des carré vous aurez le choix entre "Hex" pour Hexadécimal, "Dec" pour décimal, "Oct" pour octet et "Bin" pour binaire. Et bien pour connaitre la valeur binaire d'un nombre décimal, sélectionnez "Dec", entrez votre nombre puis sélectionnez "Bin". Ainsi vous saurez par exemple que 173 en décimal donne 1010 1101 en binaire. :)
Les différents types de variables sont basés sur les booléen (aussi appelés « Bit »).
L’octet (byte) est composé de 8 bits. Donc, en vous servant de la calculatrice windows, vous verrez que de 0000 0000 – 1111 1111 en binaire équivaut à 0 – 255 en décimal. (!!! Attention à ne pas confronte un BYTE (un octet) avec un BIT (un état binaire).
L’intéger non signé (unsigned Int) est composé de 16 bits. Donc, en vous servant de la calculatrice windows, vous verrez que de 0000 0000 0000 0000 – 1111 1111 1111 1111 en binaire équivaut à 0 – 65 535 en décimal.
L’unsigned long est composé de 32 bits. Donc, en vous servant de la calculatrice windows, vous verrez que de 0 – 1111 1111 1111 1111 1111 1111 1111 1111 en binaire équivaut à 0 – 4 294 967 295 en décimal.
On s’arrêtera là pour l’instant car ce sont les principaux types de variables, mais sachant qu’il en existe d’autres encore.
Bon c’est bien jolie tout cela mais il n’y que que des nombres positifs. Comment faire pour les négatifs?
Concentrez vous bien sur ce qui va suivre.
Pour indiquer la négation, il y a des variables particulière que nous verrons ci dessous, parmi lesquelles on utilise le bit le plus a gauche pour connaitre le signe. Lorsque celui est à 0, le nombre est positif, s’il est égal à 1, le nombre est négatif. Mais cela à une répercussion non négligeable. Le fait d’utiliser un bit de signe signifie que l’on dispose d’un bit de moins pour notre nombre. Par exemple la où un unsigned Int va de 0 à 65 535, un int « signé » (avec un signe) aura toujours 16 bits, mais 1 pour le signe, donc seulement 15 pour sa valeur. Donc si vous reprennez la calculatrice, mettez la en mode binaire et entre 111 1111 1111 1111, et vous constaterez que la valeur décimale est de 32767. Ce qui signifie que sa plage va de – 32 767 (pour 1111 1111 1111 111)1 à + 32 767 (pour 0111 1111 1111 1111).
Voici les principales variable « signée »:
L’integer (int) est une variable signée sur 16 bits allant de -32767 à + 32 767.
Le long est une variable signée sur 32 bit allant de -2 147 483 648 à +2 147 483 648.
Le float (nombre à virgule) est composé de 32 bits. Il va de -3.4028235E+38 à 3.4028235E+38. en décimal. Il y la particularité de pouvoir avoir des virgules, et ajuste automatiquement sa valeur en fonction de la précision possible.
Pour plus de précisions rendez vous directement sur site officiel d'arduino, à la page des variables: http://www.arduino.cc/en/Reference/VariableDeclaration
Ayant de nouvelles variables à disposition, on va pouvoir s’amuser avec le littéral!