Table de vérité et logique Tout Ou Rien (TOR)
Si cela était nouveau pour vous, prenez un peu de temps pour être sur d’avoir saisi les concepts précédent. Car dans cette partie, nous allons combiner les deux interrupteurs dans le même schéma et découvrirons un formidable outil servant à « rapidement » connaitre l’état d’une sortie (ampoule): la table de vérité.
Raisonnement logique Tout Ou Rien: ampoule allumée ou éteinte.
On entend par logique Tout Ou Rien (TOR) tout ce qui ne peut avoir que 2 états: l'état 0 et l'état 1.
Ce que nous faisons depuis le début du chapitre EST de la logique Tout Ou Rien (TOR), nos contacts ne pouvant être qu’au repos (=0) ou au travail (=1), aucun autre cas de figure n’est possible. Il en est de même pour notre sortie.
Alors compliquons les choses et combinons nos éléments, voilà le prochain schéma:
1 contact normalement ouvert en série avec 1 contact normalement fermé en série avec 1 sortie
Ci dessus, vous pouvez voir 1 contact normalement ouvert au repos (appelé DI1) en série avec 1 contact normalement fermé au repos (appelé DI2) et 1 sortie à 0 (appelé DO) . Deux réflexions doivent être menées de votre part:
- Combien de combinaisons d’actions différentes sont-elles possibles?
- Quelles sont les combinaisons qui alimentent la sortie? (qui allume l’ampoule)
Ce passage est très important, il faut vraiment que vous ramiez pour trouver les réponses par vous même afin que vous puissiez prendre pleinement conscience de la puissance des tables de vérités.
Bon j’espère que vous avez réussi, si ce n’est pas le cas prenez bien le temps de comprendre la solution, après analyse cela devrai vous paraître limpide après.
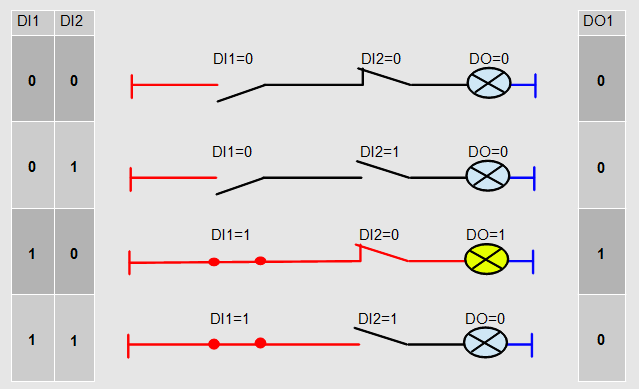
Il y a donc 4 combinaisons différentes, et les voici:
Combinaisons de 1 contact NO et 1 contact NC
Ces 4 représentations sont LE MÊME SCHÉMA mais dans 4 états différents selon les actions exercées sur les interrupteurs.
Analysons cela cas par cas:
1er cas: DI1=0 / DI2=0
Aucune action n’est exercée sur aucun contact, ceux ci sont donc tout les deux à 0. La tension positive s’arrête à DI1 et ne se connecte pas à la sortie, celle ci reste éteinte (DO=0).
On peut dire que lorsque DI1=0 et que DI2=0, alors DO=0.
2e cas: DI1=0 / DI2=1
On actionne DI2, ce contact normalement fermé passe à 1 et s’ouvre. Cela dit, la tension positive est toujours bloquée par DI1, donc cela n’alimente toujours pas notre sortie.
On peut dire que lorsque DI1=0 et que DI2=1, alors DO=0.
3e cas: DI1=1 / DI2=0
On actionne DI1, ce contact normalement ouvert se ferme et laisse passer la tension positive. Aucune action n’est exercée sur DI2, ce contact normalement fermé au repos est donc fermé et laisse lui aussi passer la tension positive. Une différence de tension apparaît donc aux bornes de la sortie, celle ci s’active.
On peut dire que lorsque DI1=1 et que DI2=0, alors DO=1.
4e cas: DI1=1 / DI2=1
On actionne DI1, ce contact normalement ouvert se ferme et laisse passer la tension positive. On actionne aussi DI2, ce qui ouvre ce contact normalement fermé au repos. Une tension positive apparaît à la gauche de DI2, mais celui ci étant ouvert, il ne la laisse pas passer. La sortie n’ayant aucune différence de tension à ses bornes reste éteinte.
On peut dire que lorsque DI1=1 et que DI2=1, alors DO=0.
Vous êtes encore la? 🙂 Ça commence à avoir un peu plus d’allure n’est ce pas? Soyez sur de maîtriser ce que l’on a vu précédemment, car ce tutoriel ladder va vous faire découvrir ce formidable outil qu’est la table de vérité.
La table de vérité, ou comment facilité la lecture du schéma.
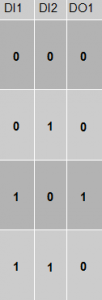
De chaque coté de nos 4 cas, vous avez du remarquer 3 colonnes, les voici reliées:
Table de vérité
Voila une table de vérité (je ne m’attarderai pas trop dessus, ceci n’étant pas le sujet du tuto, mais si cela vous intéresse demandez le sur le forum et j’essaierai de faire un article la dessus).
Le principe consiste à:
- Noter en haut des colonnes le noms des entrées et des sorties (DI1, DI2, DO)
- Pour les entrées, noter chacun de leur états possibles (étant en Tout Ou Rien, leurs valeurs ne peut être que 0 ou 1).
- Puis, dans chaque cas, regarder le schéma original, appliquez les actions nécessaire aux contacts (imaginez les à 0 ou 1) pour connaitre l’état de la sortie.
Ainsi, dans notre situation, on peut dire que notre sortie est à 1 uniquement si DI1 est au travail et DI2 est au repos, donc:
DO = DI1 ET PAS DI2
Avec cette seule équation, nous savons que l’unique possibilité pour que la sortie soit à 1 est d’exercer une action uniquement sur DI1.
Croyez moi, que lorsque les schéma se compliqueront, cela changera votre vie!
Et si on commencer à programmer?
Encore une fois soyez sur d’avoir bien compris ce qu’il s’est passé précédemment, et n’hésitez pas à poser vos questions sur le forum si vous avez des problèmes ou des remarques.
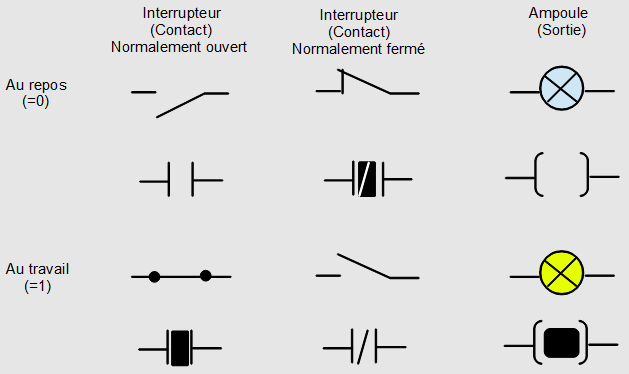
Maintenant on va faire un peu de GIMP, et on va redessiner autrement nos interrupteurs et ampoules, voici la métamorphose:
Analogie entre les symboles électrique et les symboles Ladder
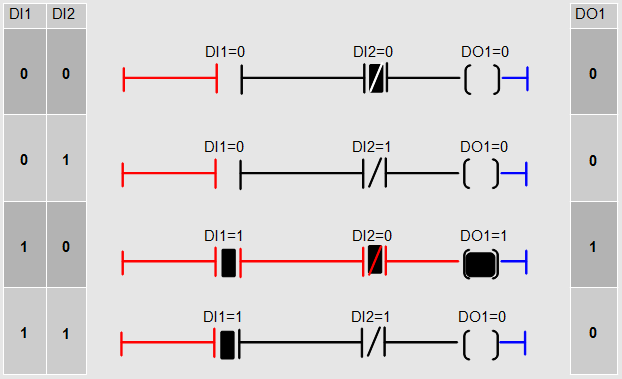
Vous reconnaissez bien sur nos contacts, avec leurs positions au repos et au travail, et en dessous vous avez la « nouvelle façon de les dessiner ». Alors vous ne serez pas supris de voir notre ancien schéma avec les 4 cas différents dessiné de cette façon:
Analogie entre les symboles électrique et les symboles Ladder – Vue des 4 cas
J’espère que cela ne vous choque pas, c’est simplement une modification « artistique » de ce qui précède. Et bien vous avez devant vous votre premier programme en ladder 🙂